Повишете точността на анализите чрез новия инструмент на Есри за филтриране на пространствена автокорелация
Пространственият анализ играе ключова роля в разкриването на сложните зависимости между географските данни. Във версия 3.4 на ArcGIS Pro са включени иновативни инструменти, които пренасят пространствената статистика на ново ниво. Сред тях се откроява възможността за филтриране на пространствената автокорелация директно от данните в полетата. Това позволява на специалистите да изолират пространствените компоненти и да разкрият истинските връзки между променливите.
Какво представлява пространствената автокорелация?
С нея се описва степента на взаимозависимост между стойностите на даден атрибут спрямо местоположението на обектите в пространството. Тази концепция е в основата на закона на Тоблер: „Всичко е свързано с всичко, но по-близките неща са по-свързани от по-далечните.“ Анализът на пространствената автокорелация позволява да се идентифицират модели на клъстериране или разпръснатост в географските данни – критичен процес за информирано вземане на решения в области като градско планиране, екология, обществено здравеопазване и др.
Какви възможности дава инструментът Filter Spatial Autocorrelation From Field?
Този инструмент позволява да се извършва по-прецизен анализ на пространствената автокорелация чрез директно филтриране на входните полета. Основните му характеристики включват:
• Персонализирани входни полета: Избор на конкретни атрибути за анализ, елиминирайки ненужния шум в данните;
• Динамичен пространствен анализ: Ефективно идентифициране на модели и клъстери, което спестява време и ресурси;
• Оптимизация на работните процеси: Намаляване на сложността и автоматизация на ключови стъпки от анализа.
Сценарии от практиката
Инструментът е изключително полезен в два основни сценария: Изследване на зависимостта между променливи и Подобряване на непространствени модели чрез пространствени компоненти.
Изследване на зависимостта между променливи
При изследване на връзката между възрастта на сградите и концентрацията на азотен оксид (NO) в Бостън първоначалният анализ показва положителна корелация (фиг. 1).
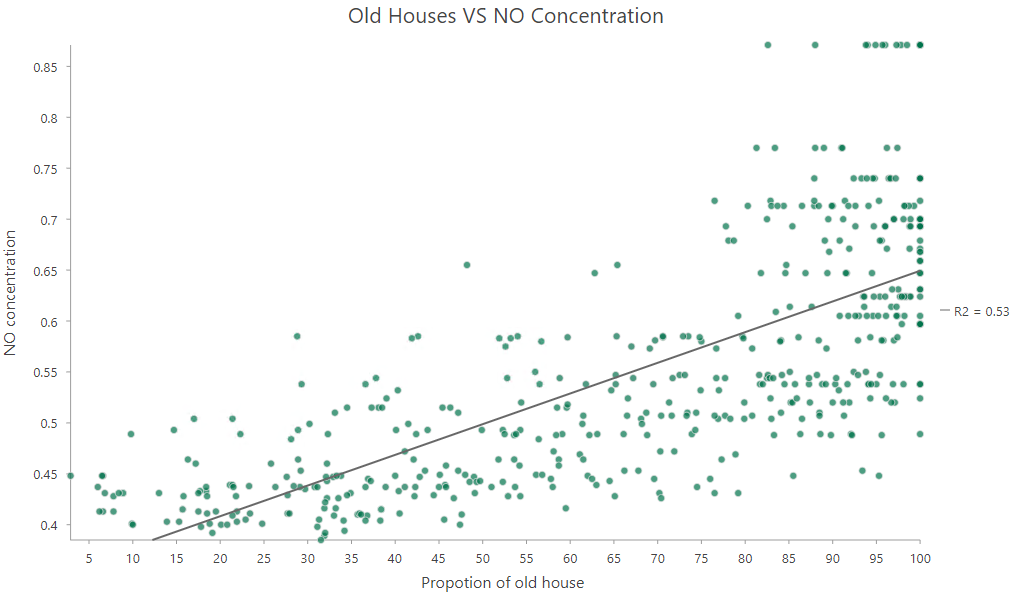
Фиг. 1. Връзката между възрастта на сградите и концентрацията на азотен оксид (NO) в Бостън
Но дали тази връзка е реална, или е резултат от пространствена автокорелация? От картите на възрастта на сградите и концентрацията на NO (фиг. 2 и фиг. 3) се вижда, че и двете променливи силно се припокриват пространствено.
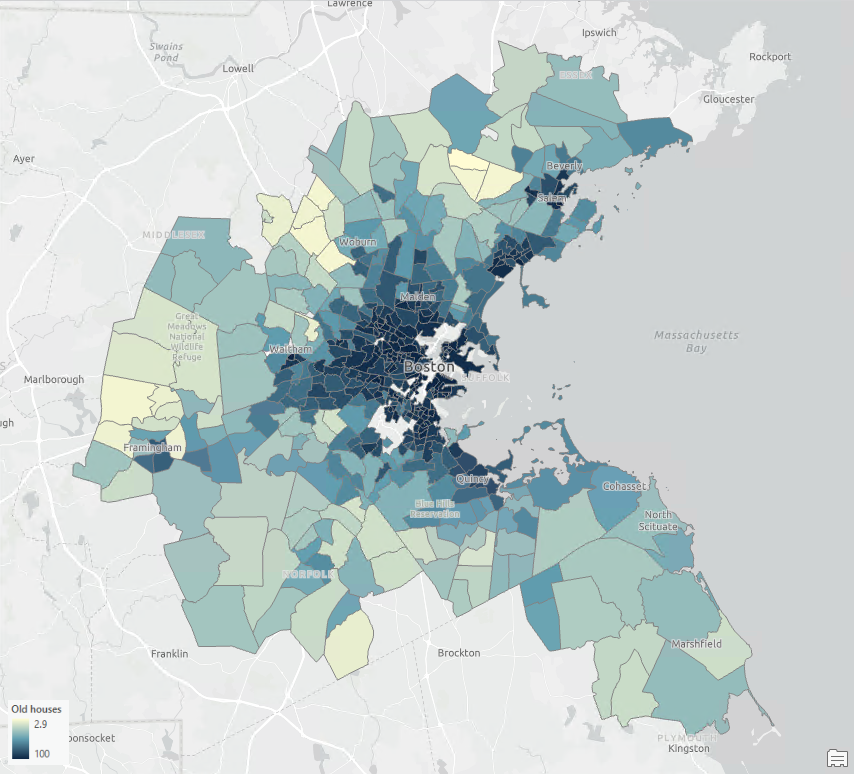
Фиг. 2. Карта на възрастта на сградите в Бостън
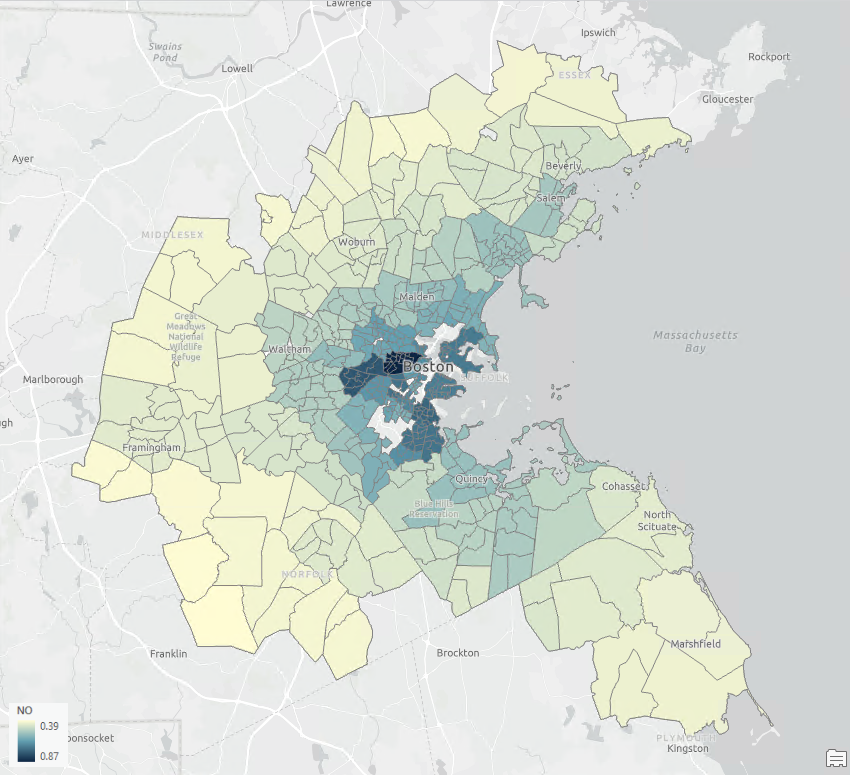
Фиг. 3. Карта на концентрацията на NO
Точно тук влиза в сила инструментът „Filter Spatial Autocorrelation From Field“. Той ви позволява да премахнете пространствения компонент от данните, за да анализирате други зависимости между променливите. За целта се:
1) Избират входните обекти (например данните за Бостън).
2) Конфигурират полетата: Избират се променливите, които ще се филтрират (като възраст на сградите и концентрация на NO).
3) Изпълнява се инструментът (фиг. 4 и фиг. 5 показват настройките).
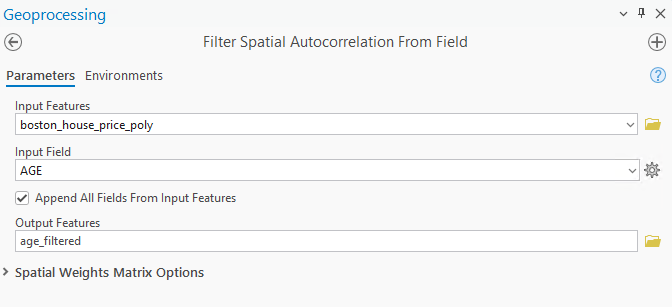
Фиг. 4. Filter Spatial Autocorrelation From Field (възраст на сградите)
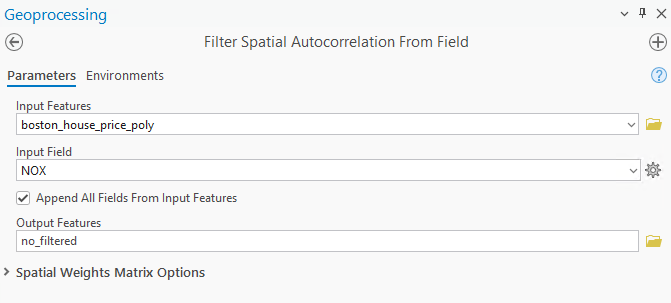
Фиг. 5. Filter Spatial Autocorrelation From Field (концентрация на азотен оксид)
След филтрирането, представяме резултатите чрез две карти:
• Филтрирана възраст на сградите (фиг. 6): Показва разпределението на възрастта без пространствената автокорелация.
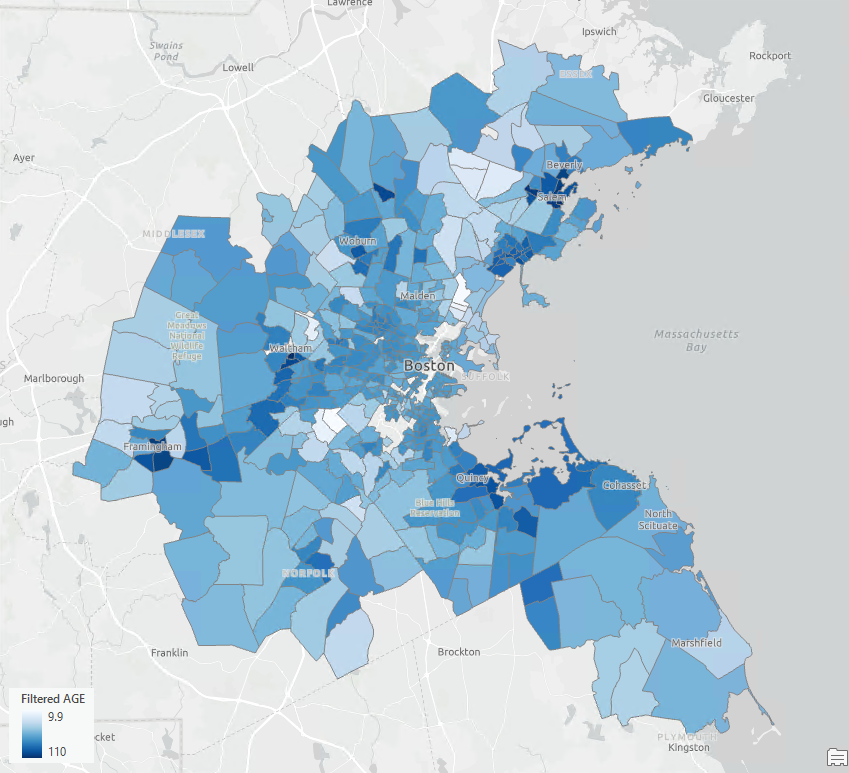
Фиг. 6. Филтрирана възраст на сградите
• Филтрирана концентрация на NO (фиг. 7): Показва концентрацията на азотен оксид без пространствени влияния.
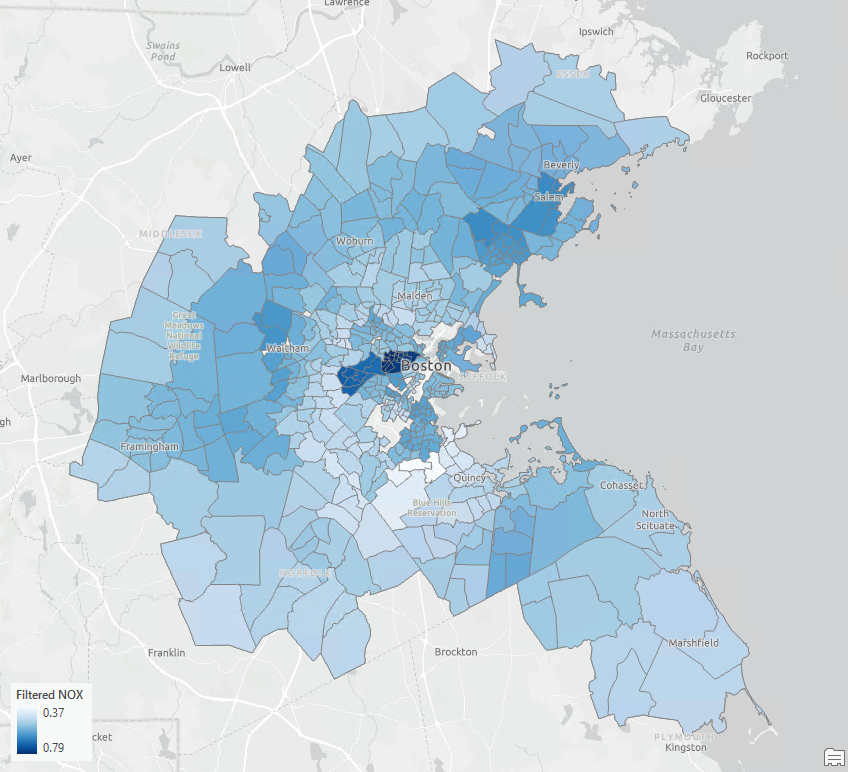
Фиг. 7. Филтрирана концентрация на NO
В резултат от филтрирането, наблюдаваме значително намаление на Moran’s I индекс – показател за пространствена автокорелация. Например за възрастта на сградите индексът намалява от 0.3206 до почти 0, което потвърждава премахването на пространствените влияния. В същото време се увеличава стойността на P-индекса, който измерва вероятността да се наблюдават дадени резултати, ако нулевата хипотеза е вярна. Казано просто, тя показва доколко резултатите от анализа са значими и дали могат да бъдат обяснени само чрез случайност. (фиг. 8).
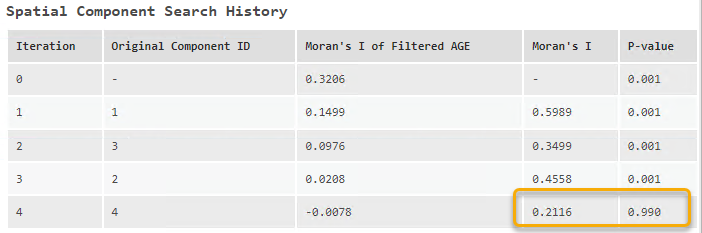
Фиг. 8. Moran’s I индекс и Р-стойност
След повторен анализ на филтрираните данни, установяваме, че първоначалната силна корелация е до голяма степен резултат от пространствени зависимости (Фиг. 9). В резултат на това се наблюдава слаба, но статистически значима връзка между двете променливи.
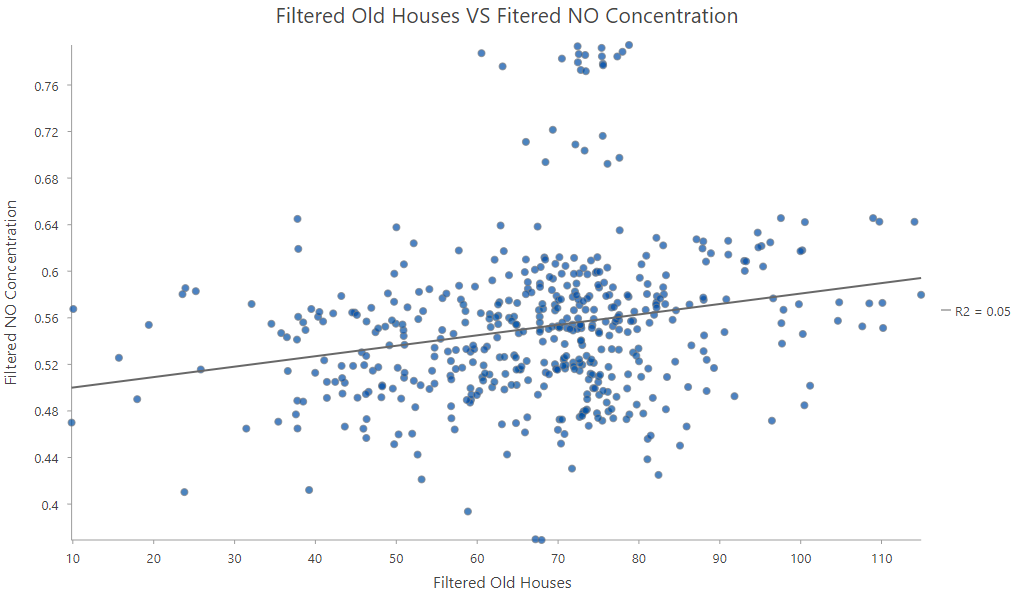
Фиг. 9. Връзката между двете филтрирани променливи
Подобряване на непространствени модели чрез пространствени компоненти
Включването на пространствени компоненти в непространствени модели позволява създаването на модели, които по-добре отразяват пространствените зависимости в данните. Нека разгледаме конкретен пример как интегрирането на пространствените резултати от инструмента Filter Spatial Autocorrelation From Field може да подобри представянето на прогнозен модел.
Създаваме горски модел, с данни за Охайо, използвайки инструмента Forest-based and Boosted Classification and Regression. Целта е да анализираме факторите, увеличаващи бедността и да прогнозираме процентите на бедност, след потенциални действия.
Целевата променлива за прогнозиране е процентът на населението, чиито доходи през последните 12 месеца са под прага на бедността (фиг. 10).
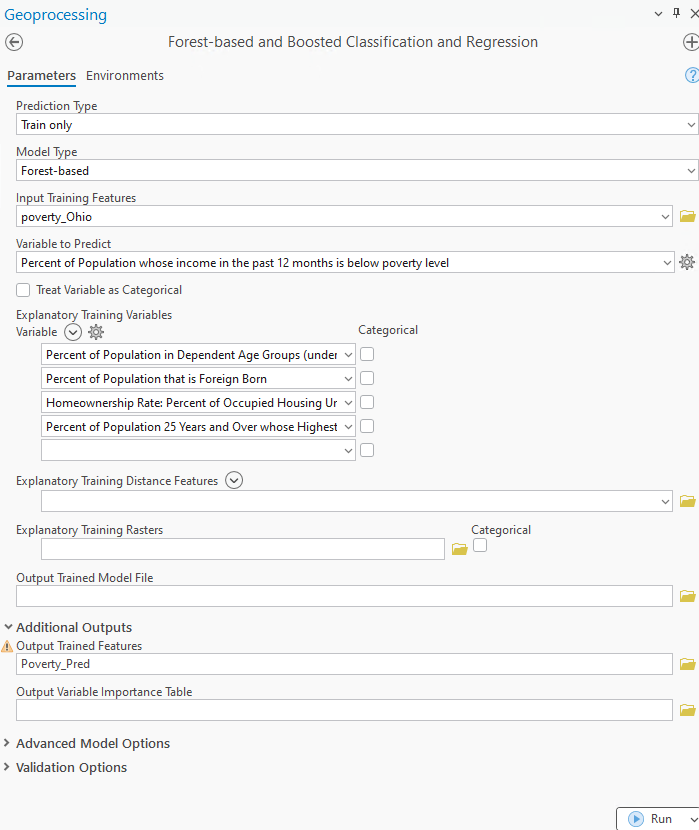
Фиг. 10. Forest-based and Boosted Classification and Regression
Разликите между наблюдаваните и прогнозираните стойности разкриват пространствена зависимост – подценяване на бедността в югоизточните райони и надценяване в северозападните (фиг. 11).
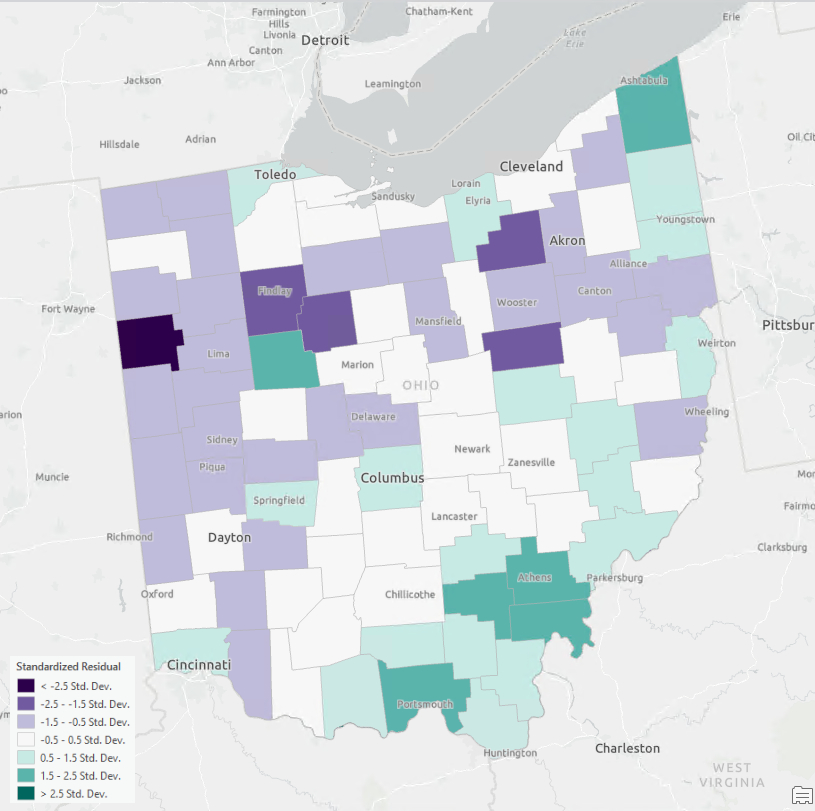
Фиг. 11. Бедността в Охайо
Тази пространствена автокорелация показа, че моделът не обяснява определени пространствени зависимости в данните. Като довод – валидиращото R² е едва 0.578 (фиг. 12).
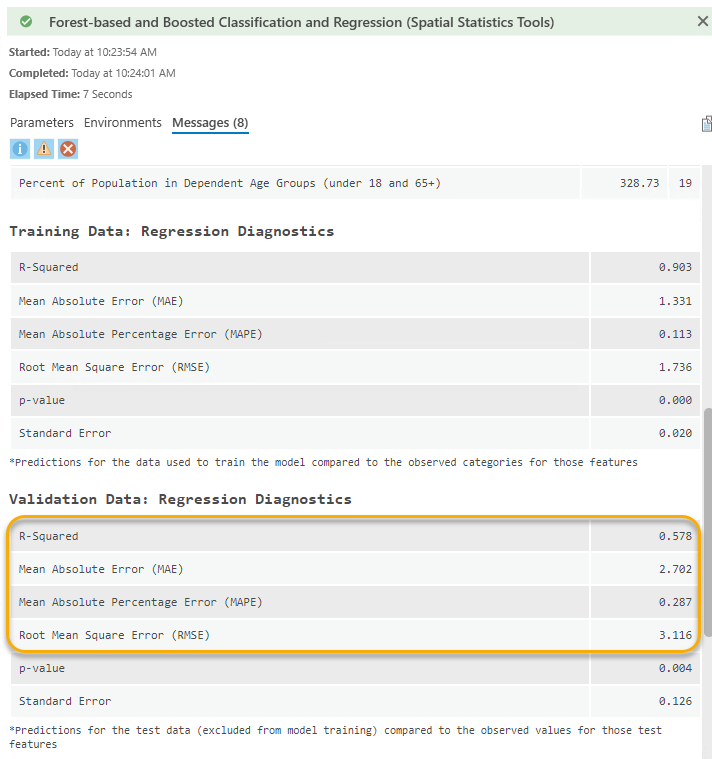
Фиг. 12. Размер на грешките
За справяне с този проблем използваме инструмента Filter Spatial Autocorrelation From Field (фиг. 13).
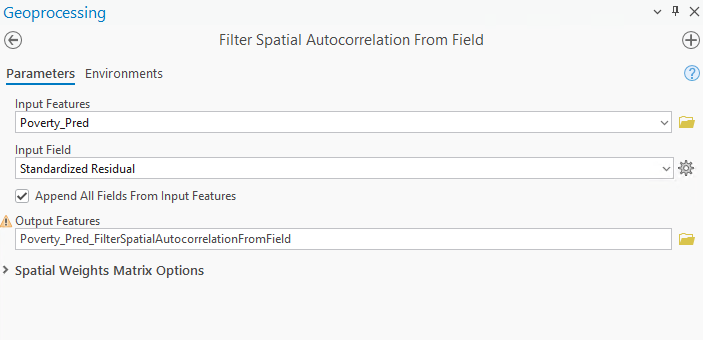
Фиг. 13. Filter Spatial Autocorrelation From Field
Получените резултати включват пространствен компонент, който няма как да бъде обяснен от горския модел. След повторно изпълнение на горския модел (фиг. 14), но този път с пространствения компонент, наблюдаваме следните подобрения:
• Валидиращото R² значително се увеличава от 0.578 до 0.819;
• Всички грешки, включително Средна абсолютна грешка (MAE), Средна абсолютна процентна грешка (MAPE) и Коренна средна квадратична грешка (RMSE) са значително намалени (фиг. 15).
• Пространственият компонент се оказа най-важната обяснителна променлива (фиг. 16).
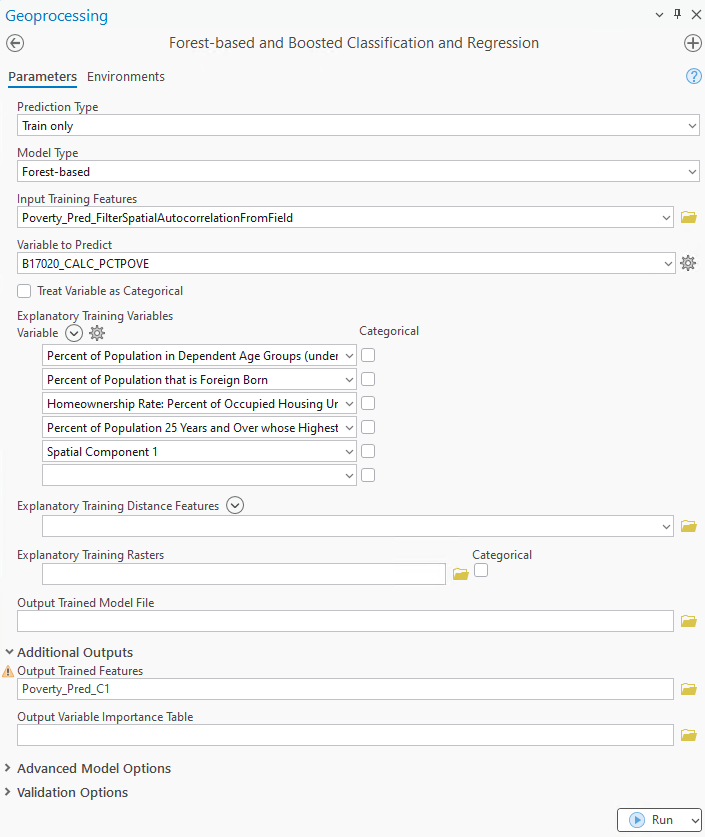
Фиг. 14. Горският модел с пространствена компонента
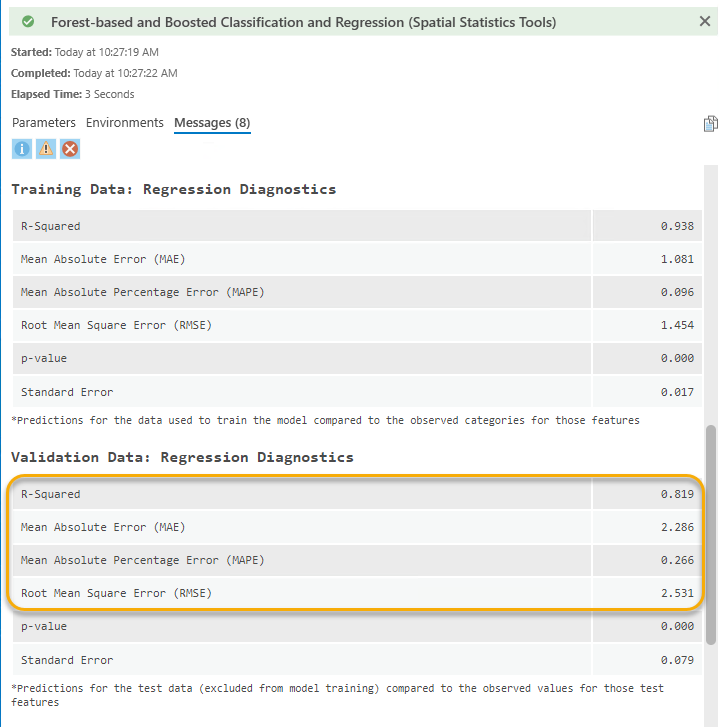
Фиг. 15. Грешки
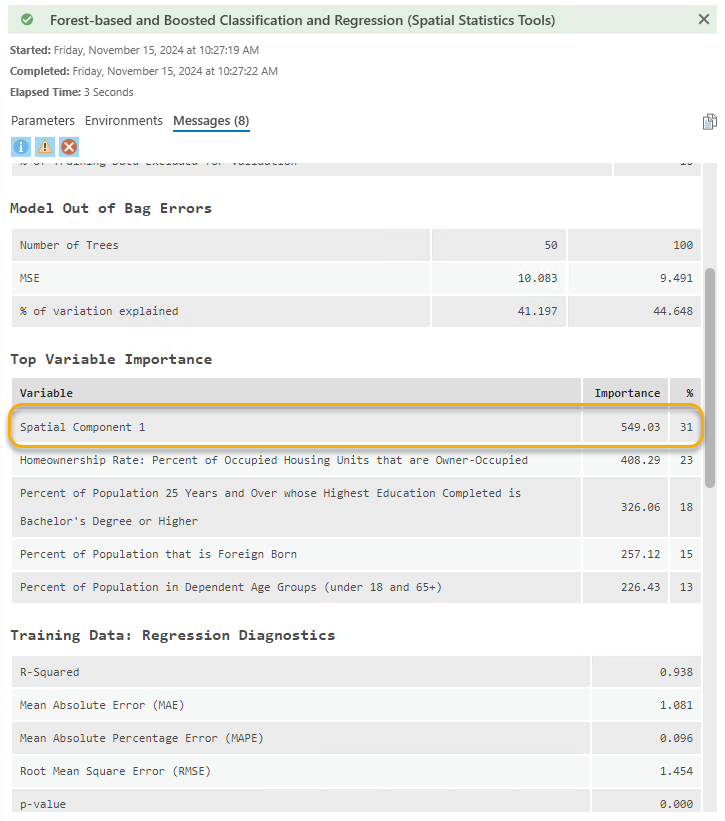
Фиг. 16. Значимост на компонентите
Изобразени върху карта, резултатите представят по-високи стойности на бедността в югоизточната част на Охайо и по-ниски - в северозападната част на щата (фиг. 17). Тези резултати предопределят бъдещите действия за намаляване на бедността и съсредоточаване на усилията в югоизточния район.
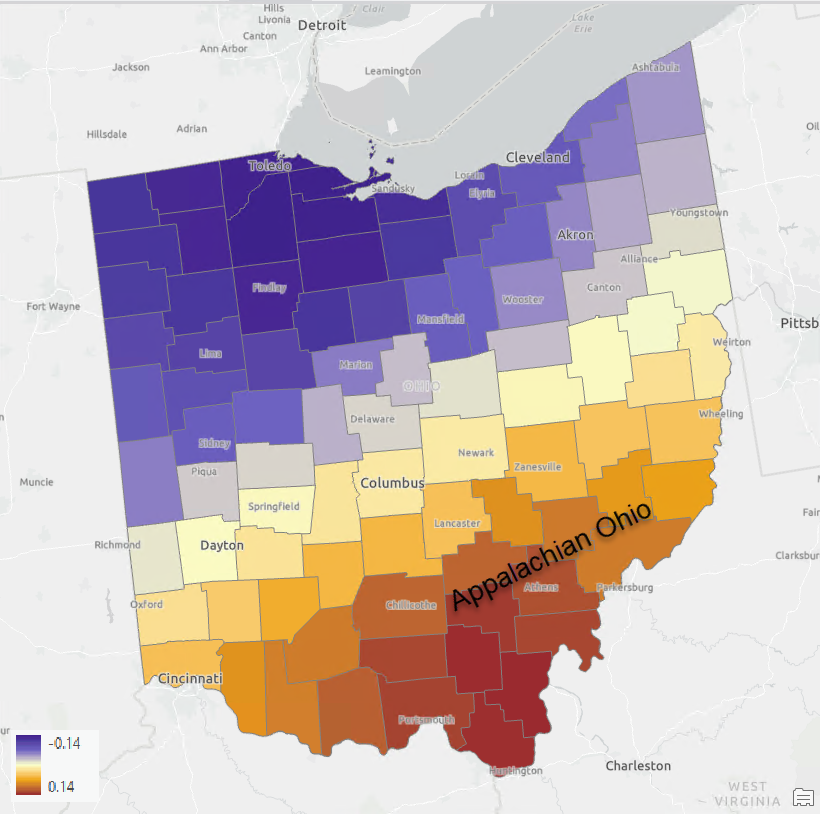
Фиг. 17. Бедността в Охайо
Чрез интегрирането на пространствени компоненти в непространствени модели можем да подобрим тяхната надеждност и да уловим пространствени процеси, които иначе биха останали незабелязани. Този подход не само подобрява представянето на модела, но и предоставя по-дълбоки прозрения за пространствените феномени, което улеснява по-целенасоченото и ефективно вземане на решения.
За да се възползвате от този нов инструмент, уверете се, че разполагате с версия ArcGIS Pro 3.4. Отворете набора от инструменти за пространствена статистика Spatial Component Utilities и изберете инструмента Filter Spatial Autocorrelation From Field. Следвайте описаните стъпки на работния процес, за да персонализирате анализа спрямо вашия набор от данни.
###